hi all,
new to the board, please be gentle 🙂
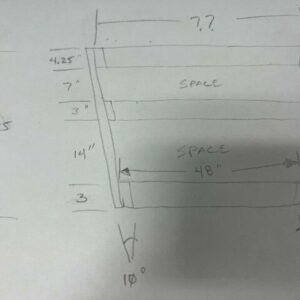
hobbyist wood worker here who needs some math help. Attached is a drawing of a piece i’ll be building this weekend. you can see the total height of the piece will be 31.25 inches.
please pay no mind to the center board…
the sides will have a 10 degree slant from the bottom to the top. if the top of the bottom shelf is 48 inches wide and the top of the top shelf is 28.25 inches away, how wide should that top board be with the 10 degree slants?
any help is appreciated!














Replies
I’m going to say more than a smidgen (that’s a smidge in metric) and less than a tad. Woodworking is great for the brain :)
Math? We don't need no stinking math. Too many things can go wrong.
Cut your sides to size. Cut your bottom shelf to size, with 10 degree angles on the end. Cut your top shelf overlong, with a 10 degree bevel on one end. Put the bottom shelf in place, then mark the top shelf and cut.
Try always to mark, not measure.
thanks guys, that was the route i was going to go and just thought i'd ask.
i appreciate the smidgen of feedback :)
Each end of the upper shelf will be longer by 28.25 times tangent(10º). Tangent(10º) = 0.1763. So total length = 48 + 2(4.98) = 57.96. That's a little more than 1/32" shorter than 58".
Having done all that, it is also easy to make a full scale or half scale drawing and measure the distance directly. You just need a good way to draw the 10º angle. Sometimes that is easiest to do accurately by using the tangent and the distance, which means you would do the above calculation first, which then means that you might not need the drawing...
With a 10 degrees slant, each side will reduce or lengthen by 5,02 inches making the top 38 inches if slant is inwards. I used 28,5 inches by mistake, with 28,25 inches height, it’s like the previous calculation, 4,98 inches per side.
you just gave me a head ache jharveyb but i do appreciate the answer!
Buy a roll of underlayment paper and draw a full size model.
Measure the top board on the drawing.
The less math the better. Adopt story sticks, full-size layouts, and cut to fit assembly. Save the simple math for how much lumber you need, from where, and at what price.
Nope, no math. In ww'ing you need to learn to work from reality.
Cut the bottom, lay the sides and bottom down on a table, clamp the sides to the bottom and measure the longest or shortest distance for the top. If its not perfect, you schooch it up or down till it fits.
You're gonna want to make some clamping blocks. Glue (not double stick) some 80 grit sandpaper on it.
Another mathematical approach to calculate the amount of tapering due to an angle we used prior to the widespread use of CAD and personal computers of cell phones is this simple arithmetics. For every degree of angle there will be a 17 thousands of an inch deflection for every inch of length (actually closer to 17,6) so in our case, for a 28,25 inches distance at 10 degree slope the deflection will be 28,25 X 10 X 0,00176 = 4,97 inches.
A word of caution: This method only works for small angles.
You must be right, we used it in mold making design and repair to estimate how the size of a component would increase due to draft angles which were around 5 degrees. I recall we used 17 thousands per inch per degree and that is probably why with ten degrees 0,176 was necessary to approach the true value.
Agree with above about cutting the bottom one at 48" and then laying out.
I routinely use Sketchup to draw these types of things and it works very well, no math needed. Looks like the top would be 38-3/16"
This forum post is now archived. Commenting has been disabled