How to Draw an Ellipse
Bob Miller argues that with a few simple formulas and a clever jig, it becomes possible to draw and cut ellipses of any size and add this stately and pleasing shape to your work.
An ellipse is a special kind of oval, in fact it’s the most stately and refined of the ovals. What sets the ellipse apart from other ovals is that it can be mathematically defined and mechanically drawn. Most people will look at an ellipse and simply call it an oval, but there is more to it than that. With a few simple formulas and a clever jig, you can draw and cut ellipses of any size and add this stately and pleasing shape to your work.
What makes an ellipse special is two points inside the shape called the “foci” (plural of “focus”). What makes them important is that the distance between the focus, the edge, and the other focus is constant for any point on the perimeter of the ellipse. Not only does this result in an elegant and pleasing shape, but it also allows the ellipse to be drawn precisely and easily.
Since it is possible to define an ellipse mathematically, this is where some math comes in. But don’t worry; you can do it. All you need to know is the overall size of the ellipse, defined by its length and width at its maximum points. These two dimensions are called the major axis and the minor axis. From there it is possible find the location of the foci, using this formula:
C=√(A2-B2)
where C equals the distance between the center and each of the foci and A equals the radius of the major axis and B equals the radius of the minor axis. See the diagram below to see what goes where.
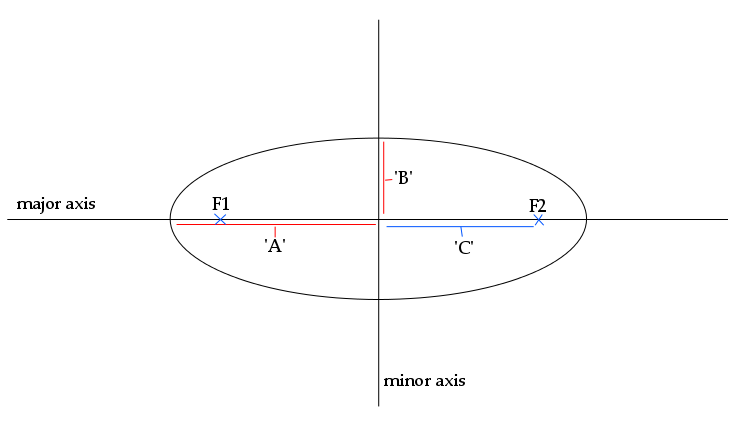
Once you know where the foci are located relative to the center of the ellipse, drawing the ellipse becomes a d0ddle.
Simply drive two nails into the pattern at the foci, and tie a loop of non-elastic string that hooks on both foci and when pulled taut reaches to any point on the ellipse. Then simply keeping the loop of string taut, move the pencil around the foci, letting the string guide your path. Because the string is a fixed length, it will keep the pencil equidistant from both foci and will neatly and cleanly define an ellipse. See the following diagram and video for how this works.
While the string method is great for drawings and layout, to actually cut a precise ellipse you will need an ellipsograph, a clever jig that can move in an elliptical shape and carry anything from a pencil to a router. The ellipsograph is quite simple; all is required is two dovetailed tracks in MDF that are perpendicular to each other. Two pieces of hardwood are then milled to a sliding fit in the tracks and a bolt added at their centers.
Attach a rigid plywood arm to both bolts. To control the size of the ellipse, you need to know the major and minor radius of the ellipse (A & B from the formula above). Attach a router to the plywood arm and then attach it to the two sliding blocks. Attach one block the minor distance from the router and the other the major distance from the router. As you maneuver the arm around the ellipse, the two sliders will bypass each other in the jig and move the end of the arm in a perfect ellipse!
Don’t fear the ellipse, and don’t fear the doing the math to make it happen.
Fine Woodworking Recommended Products
Ridgid EB4424 Oscillating Spindle/Belt Sander
Circle Guide
Drafting Tools
Comments
Bob thanks
I needed to make a template for routing out a number of elliptical recesses to locate folding D rings in a deck. Your formula does the trick. Big question I have is how do you "Attach a router to the plywood arm" when it is pretty clear the corners of the ellipsograph will block the travel of the router base. Could you post a picture of your rig with the router attached and showing the path around the jigs hard corners...?
Log in or create an account to post a comment.
Sign up Log in